|
|
做题情况
选择错1
值得注意的题
123都是常规的计算题.因为做法很显然,所以做这类题应该以正确率为主,适当放慢计算速度未必不可
4.其实也是计算题.没想到选择题会出成大题的样子.做法就是传统的斯托克斯然后投影一下
5.令 A=(\alpha,\beta,\gamma) 只需注意到所给的矩阵是 A 的若干次初等变换的结果.即
(\alpha+ \beta,\beta + \gamma,\gamma + \alpha) = (\alpha,\beta,\gamma) \begin{pmatrix} 1 & 0 & 1\\ 1 & 1 & 0\\ 0 & 1 & 1\\ \end{pmatrix} . (\alpha + 2\beta,\beta + 2\gamma,\gamma + 2\alpha) = (\alpha,\beta,\gamma)\begin{pmatrix} 1 & 0 & 2\\ 2 & 1 & 0\\ 0 & 2 & 1 \end{pmatrix}
6.和15一样不太懂,感觉纯计算好像没啥意义(?)
8.感觉是好题.
直觉选了B. 1的错误是显然的,只需要令 C=A . 我觉得此题意义主要在于学习做这类题的构造反例思路.
13.看到分段函数不论偏导是否存在都直接考虑用定义肯定不会错
18.本题就是求 (b-a)^4,a \leq 0,b \geq 0 在 \frac{a^2}{2}+b^2 = 1 下的最大/小值
令 \begin{cases} x = -\frac{1}{\sqrt{2}}a\\ y=b \end{cases} ,即有 x^2+y^2 = 1 \quad (x,y\geq 0)
.考虑 f(x)=x^4 [0,+\infty) 上为偶函数.只需求 \sqrt{2}x+y 的最值.
此时可以采用三角换元/判别式法/平均值不等式/拉格朗日乘数法等方法.这次用线性规划(未必是最简单的).
令 z = \sqrt{2}x+y .将其看作 xoy 面的斜截式方程,即 y = -\sqrt{2}x + z .这条直线的截距就是所求的值.显然当直线恰好与圆相切时取到最大值,当直线经过 (0,1) 时取到最小值.
故最小值 z=1 .当 x=0,y=1 时取得.
对 x^2+y^2=1 两边求导. \begin{cases}2x + 2yy^{'}=0 \\y^{'} = -\sqrt{2}\\ x^2+y^2=1 \end{cases} 得到 x=\frac{\sqrt{6}}{3},y=\frac{\sqrt{3}}{3},z=\sqrt{3} .
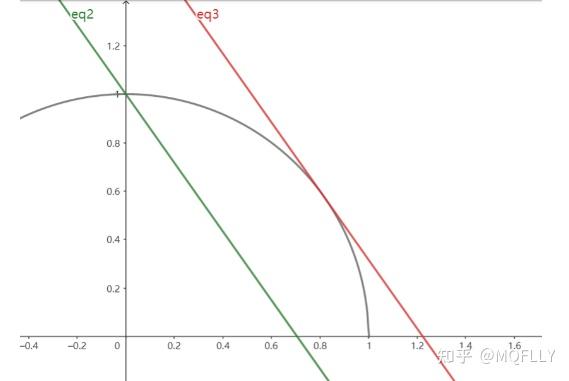
左边的曲线实际上不存在
19.和李林的某道物理题一样,感觉都是高中物理题.不明白大题为什么要出这个
21.先说一下看法:无论有没有做出来我觉得都仅作了解即可.真题考得概率比较低,因为我觉得这样的题出来对于学过相关知识同学来说就是很大的便宜,没学过就很难做出来.这样的考法我觉得不适合考研.
这题的背景是数值分析/矩阵论的中的 \text{QR} 分解或酉-三角分解 它指出任意的 A \in C^{n \times n} 都可以作 \text{QR} 分解.常用的方法有householder变换,Givens变换,还有本题的Schmindt正交化方法.
我觉得本题最大的意义就是让你捡回Schmindt正交化,并且探索Schmindt正交化的几何直观.下面试证明上述命题成立
由Schmindt正交化.
\begin{cases} \beta_1 = \alpha_1\\ \beta_2 = \alpha_2 - \frac{(\alpha_2,\beta_1)}{||\beta_1||^2}\beta_1\\ \beta_3 = \alpha_3 - \frac{(\alpha_3,\beta_1)}{||\beta_1||^2}\beta_1 - \frac{(\alpha_3,\beta_2)}{||\beta_2||^2}\beta_2 \end{cases} .如何理解这个过程.以 \beta_2 的过程为例就是在 \beta_1 的基础上构造了 \alpha_2 在 \alpha_1 方向上的投影.然后相减就得到了正交的 \beta_2
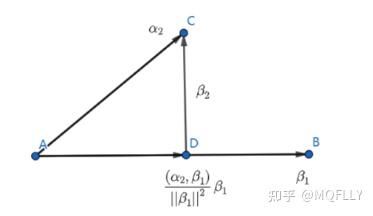
不妨记 \lambda_{i,j} = \frac{(\alpha_i,\beta_j)}{(\beta_j,\beta_i)} ,由上知,这就是投影
于是有
\begin{cases} \beta_1 = \alpha_1\\ \beta_2 = \alpha_2 - \lambda_{2,1}\beta_1\\ ...\\ \beta_n = \alpha_n - \sum_{i=1}^{n-1} \lambda_{n,i} \beta_i \end{cases} .下面进行单位化.有 \begin{cases} \gamma_1 = \frac{\beta_1}{||\beta_1||}\Rightarrow \alpha_1 = \gamma_1||\beta_1||\\ \gamma_2= \frac{\beta_2}{||\beta_2||} \Rightarrow \alpha_2 =\lambda_{2,1} ||\beta_2||\gamma_1 + ||\beta_2||\gamma_2\\ ...\\ \gamma_n = \frac{\beta_n}{||\beta_n||} \Rightarrow \alpha_n = \sum_{i=1}^{n-1} \lambda_{n,i}||\beta_i||\gamma_i + \gamma_n ||\beta_n|| \end{cases}
于是 (\alpha_1,\alpha_2...\alpha_n) = (\gamma_1,\gamma_2...\gamma_n) \begin{pmatrix} ||\beta_1|| & \dots & \lambda_{n,1} ||\beta_1||\\ & \ddots & \vdots\\ & &||\beta_n|| \end{pmatrix}_{n \times n}
与是两问都可以直接写出结果.本质上是进行了"逆"Schmindt正交化的过程
总结
感觉这张难度主要在计算量,除了8以外实在找不出比较创新的题了.大题出得有点神秘,质量感觉不如填选.基本填选就能反映计算能力过不过关吧. |
|