关于一道高中数学题分析与总结

文化兔子

先来看题：
若有函数 f(x)=\log_a(x+2)+\log_a(2-x),0<a<1 ，
则： 1) 判断该函数的奇偶性。
2) 若该函数最小值为 -2 ，求 a 的值。
欧克欧克，解这道题，咱们首先关注到不那么“寻常”的一点： 0<a<1 。
这一点说明什么，我们知道，如果 a\in(0,1) ，那么 \begin{cases} a^x<a,x>1\\[2ex] a^x>a,0<x<1\\ \end{cases} 。
我们在把这个函数拆一拆，化简一下，想必是个人都会。。
f(x)=\log_a(2+x)+\log_a(2-x)
=\log_a[(2+x)(2-x)]
=\log_a(4-x^2)
然后呢，我们先看原函数哈，是不是要让这个函数有意义，那么就要：
\begin{cases} 2-x>0,x<2\\[2ex] x+2>0,x>-2\\[2ex] \end{cases} ，综上， -2<x<2 ，即该函数定义域为 (-2,2) 。
那么，分析完一波，我们先来解决第一小问，这个函数是奇函数还是偶函数？
偶函数是什么？两边对称的，也就是满足 f(x)=f(-x) 的函数。
我们来算算，这个函数我们已经化简成 f(x)=\log_a(4-x^2) 了，那这不是很简单？
因为有 (-x)^2=x^2 ，所以——
f(x)=f(-x)=\log_a(4-x^2) 。
即该函数是偶函数。
或者不化简也可以，直接来算：
f(x)=\log_a(x+2)+\log_a(2-x) ，
f(-x)=\log_a(2+(-x))+\log_a(2-(-x))=\log_a(x+2)+\log_a(2-x) ，
\therefore f(x)=f(-x) ，
\therefore 该函数是偶函数。
接下来解决第二小问：
我们已经把这个函数化简成：
f(x)=\log_a(4-x^2) 。
那么接下来，我们为了计算方便，可以假设 m=4-x^2 ，
那么，原函数就化为 f(x)=\log_am 。
那么接下来，最关键的一点来了，
首先，给大家打个预防针，我在接下来会很“啰嗦”，会从对数的定义开始分析，勿喷，谢谢！
我们知道，对数函数，是由 a^x=N ，延伸出来
\log_aN=x 。
也就是说，对数函数是求指数的一种函数。我们把上式中 a 称为底数， N 称为真数。
在这里，它的底数 a\in(0,1) ，即底数是纯小数。
我们知道，纯小数的幂有一个特性：只要是大于一次的幂，永远比底数小；小于一次的幂，永远比底数大；等于一次的就不用说了。
接下来，我们知道这个函数的底数小于 1 ，所以 m 越大， f(x) 的值反而越小，可以参照下图：


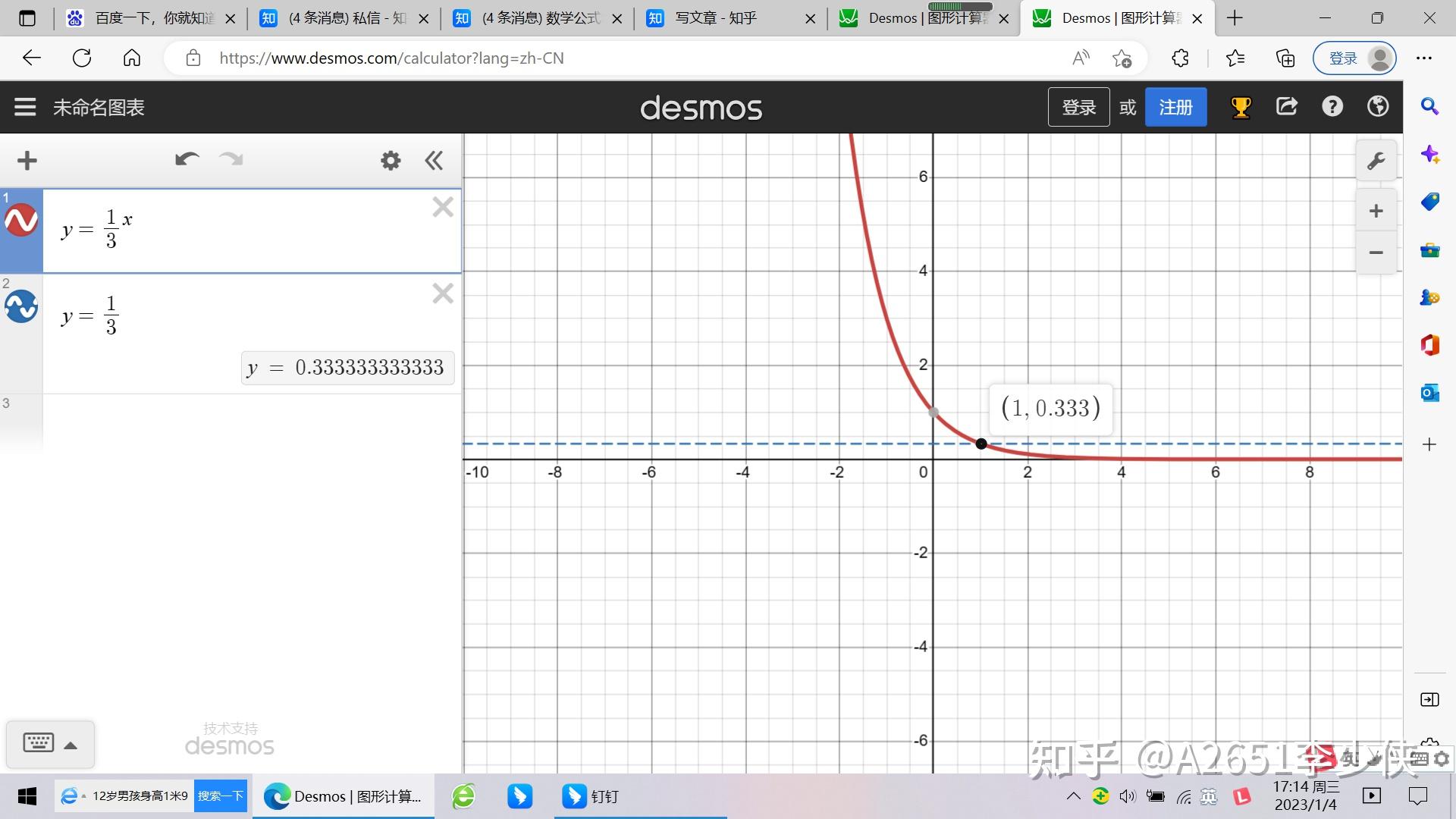
所以呢，我们知道了函数的最小值，对应的，我们就要求出 m 的最大值。
这时， m 的最大值就对应了 f(x) 的最小值，即 -2 。
我们知道， m=4-x^2 ，那么 x^2 的最小值，就是 m 的最大值。
x^2 的最小值，就是 \left|x\right| 的最小值咯，是——
\Large0 ！！！！！！！！！！！！
没错，大鸭蛋。。。咳咳
所以这时候，也就是 x=0 时， m=4-x^2 达到最大值 m=4 。
此时，原函数变成 \log_a4=-2 ，
进一步地，解方程，我们可以得到 a=\frac{1}{2} 。
接下来，标准、完整地写下整个解题过程：
解：原函数可化简为： f(x)=\log_a(4-x^2).
1) \because x^2=(-x)^2,
\therefore \log_a(4-x^2)=\log_a(4-(-x)^2),
即 f(x)=f(-x),
\therefore 原函数为偶函数。
2) 令 m=4-x^2,  
则原函数化为 f(x)=\log_am.
\because0<a<1,
\therefore m 取最大值的时候， f(x) 达到最小值 .
\because f(x) 的最小值为 -2,
m 的最大值为 x=0 时 m 的值，即 4.
\therefore  可列出方程 \log_a4=-2 ，
解得 a=\frac{1}{2}.
Q.E.D.
好啦，现在可以看图啦！


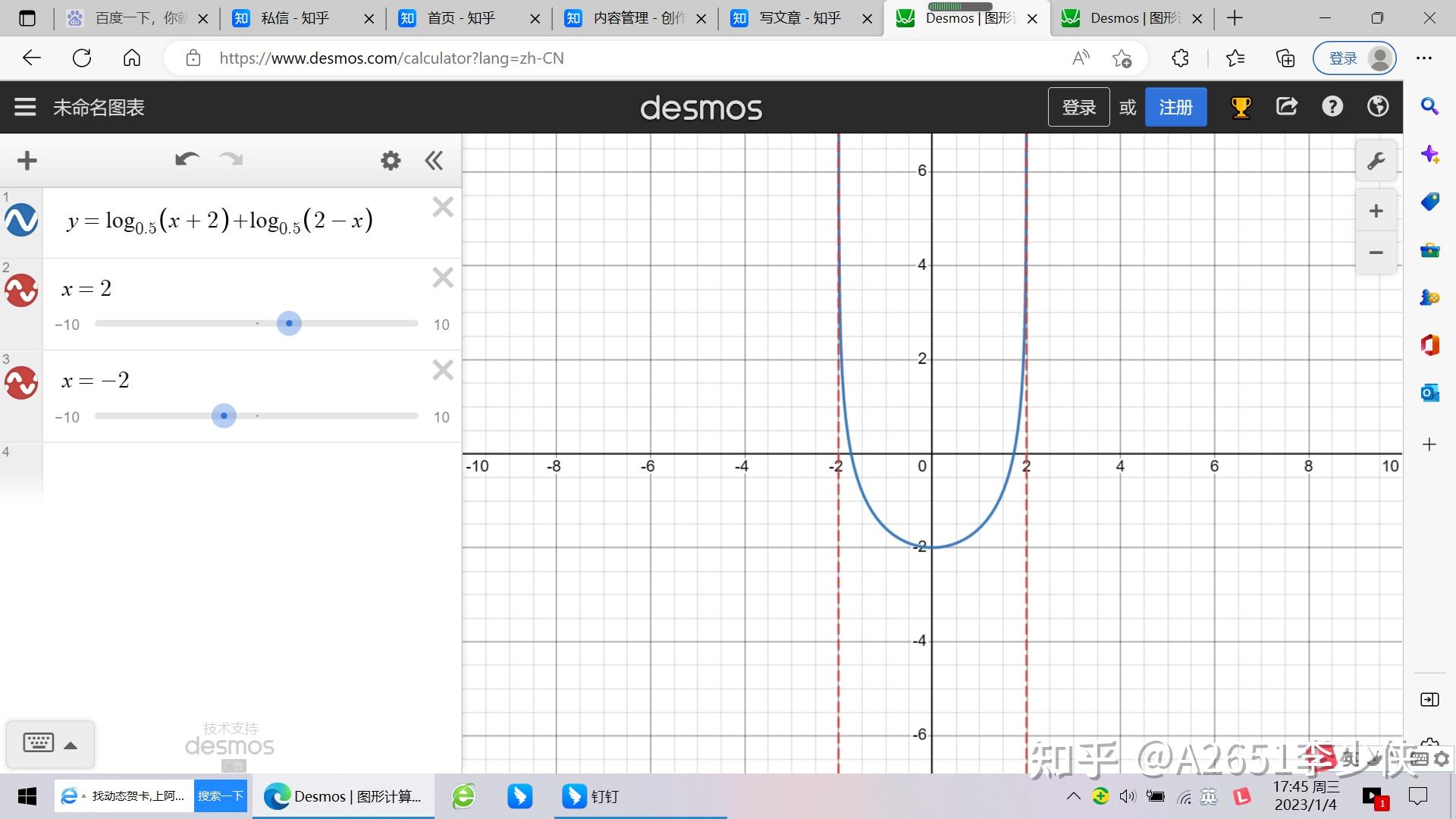
总结：这题主要考察奇偶性的判断，以及对数函数性质的运用，总体来说难度偏简单。
欧克，每日一题，预防老年痴呆，各位，再见！